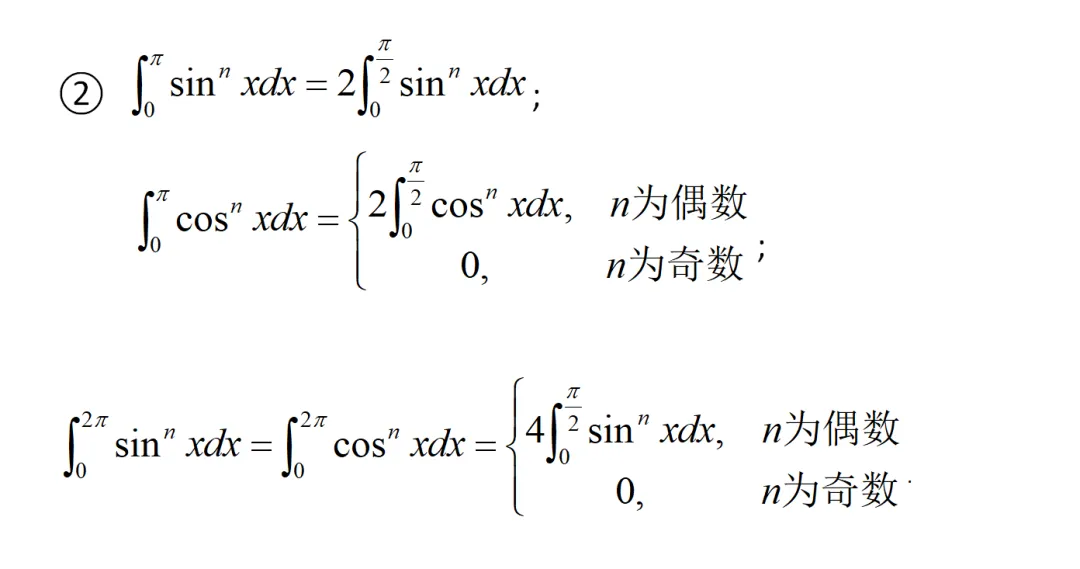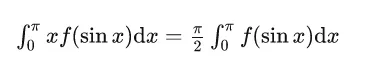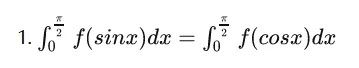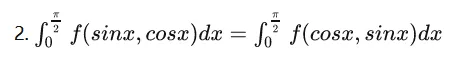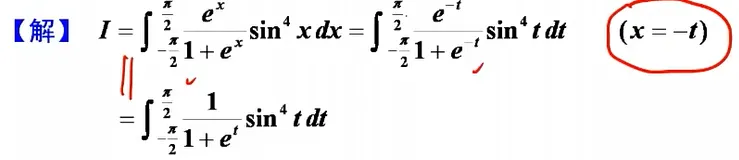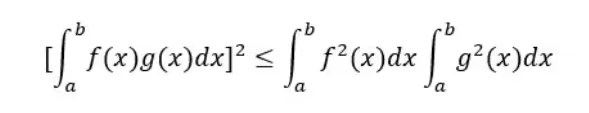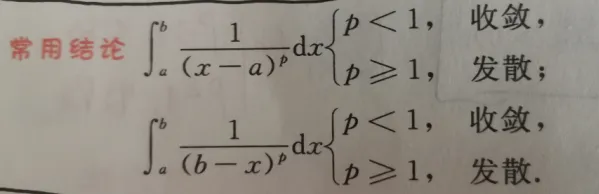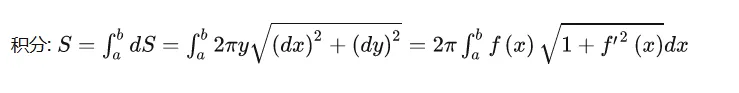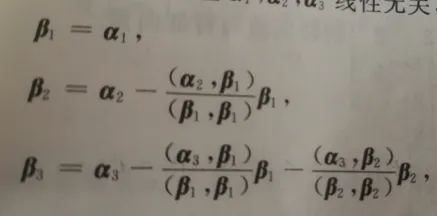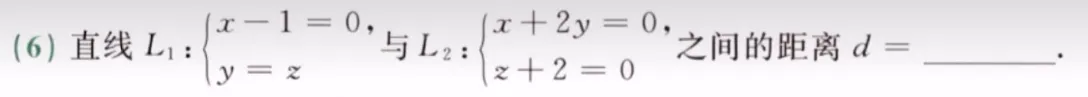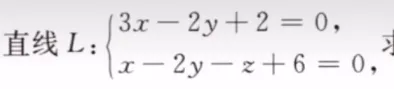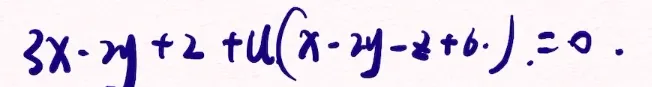高等数学
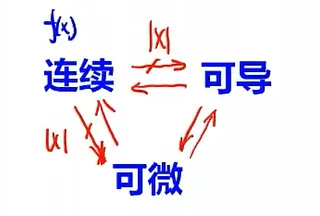
函数极限连续
周期函数的导函数是周期函数,反之不一定。
有界性判断定义3:导函数在有限区间有界—>函数有界
无穷大×无穷大=无穷大 无界×无界≠无界
p16 重要极限x^n 和 e^nx
==泰勒公式p18==
根式除以-x p24
==数列的极限==
1.对数列求极限不能用洛必达法则,必须改成函数极限
2.递推关系数列xn+1=f(xn)常用方法:①单调有界,等式两端取极限 ②先斩后奏,令极限为A,两端取极限解出来,再证明极限是A,方法:n->∞,|xn-A|<缩放因子*|xn-1 - A|=…=0
3.判断单调性:①若f(x)在I上单增,则数列{Xn}单调,当x1≤X2时,{Xn}单增,当x1≥X2时,{Xn}单减。②f(x)单减->{Xn}不单调
均值不等式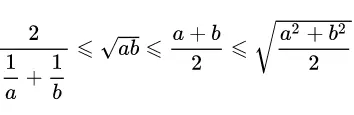 乘积开根号≤均值≤平方的均值开根号
乘积开根号≤均值≤平方的均值开根号
一元函数微分学
①f(x) n阶可导–>洛必达最多洛到n-1阶
②f(x)n阶连续可导/有n阶连续导数–>可以洛到n阶
==cot导数-csc^2 csc导数-csccot==
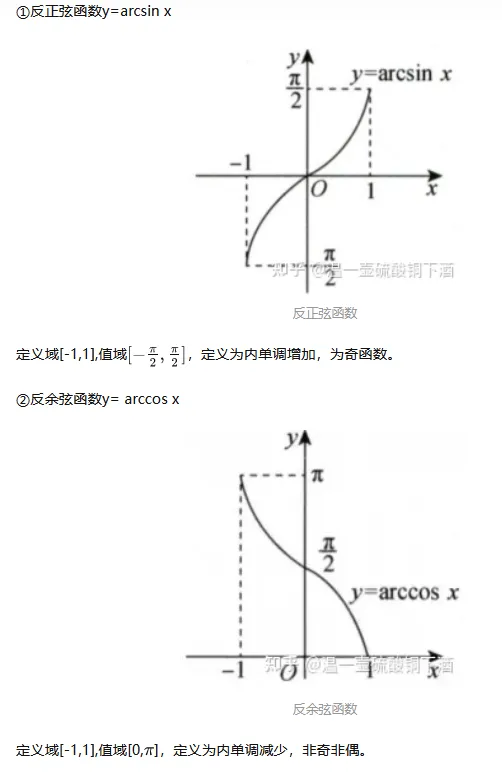
arcsin,arccos,==arccot导数==
arctanx+arctan(1/x) = Π/2
p57
==微分中值定理大题专题== ⭐构造辅助函数法p83
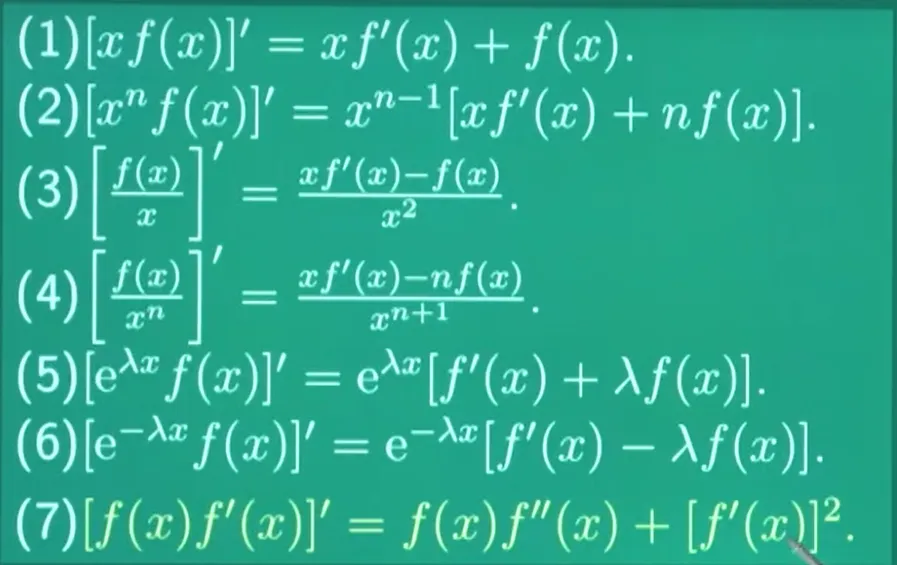
极值和拐点的第三充分条件p68 p69
⭐罗尔定理推论:若在区间I上f(x)的n阶导数≠0,则方程f(x)=0在I上最多有n个实根
一元函数积分学
不定积分

万能代换 
定积分可积性
点火公式
区间再现
三角函数积分一般方法
但此题用上面区间再现的公式做更快
e的x次方用区间再现
==变上限积分函数==
积分不等式
==柯西积分不等式==
乘积积分的平方不超过平方积分的乘积
提到单调性,改用变上限积分用函数的思想证明积分不等式
反常积分
1.收敛+收敛才收敛, 其中一个发散则发散
2.p积分
3.

例子:


定积分的几何应用
旋转体体积:
、
旋转体侧面积:
物理应用p32:
1.变力做功 2.液体压力 3.引力
常微分方程
伯努利方程 欧拉方程p141 欧拉方程的另一种解法p169
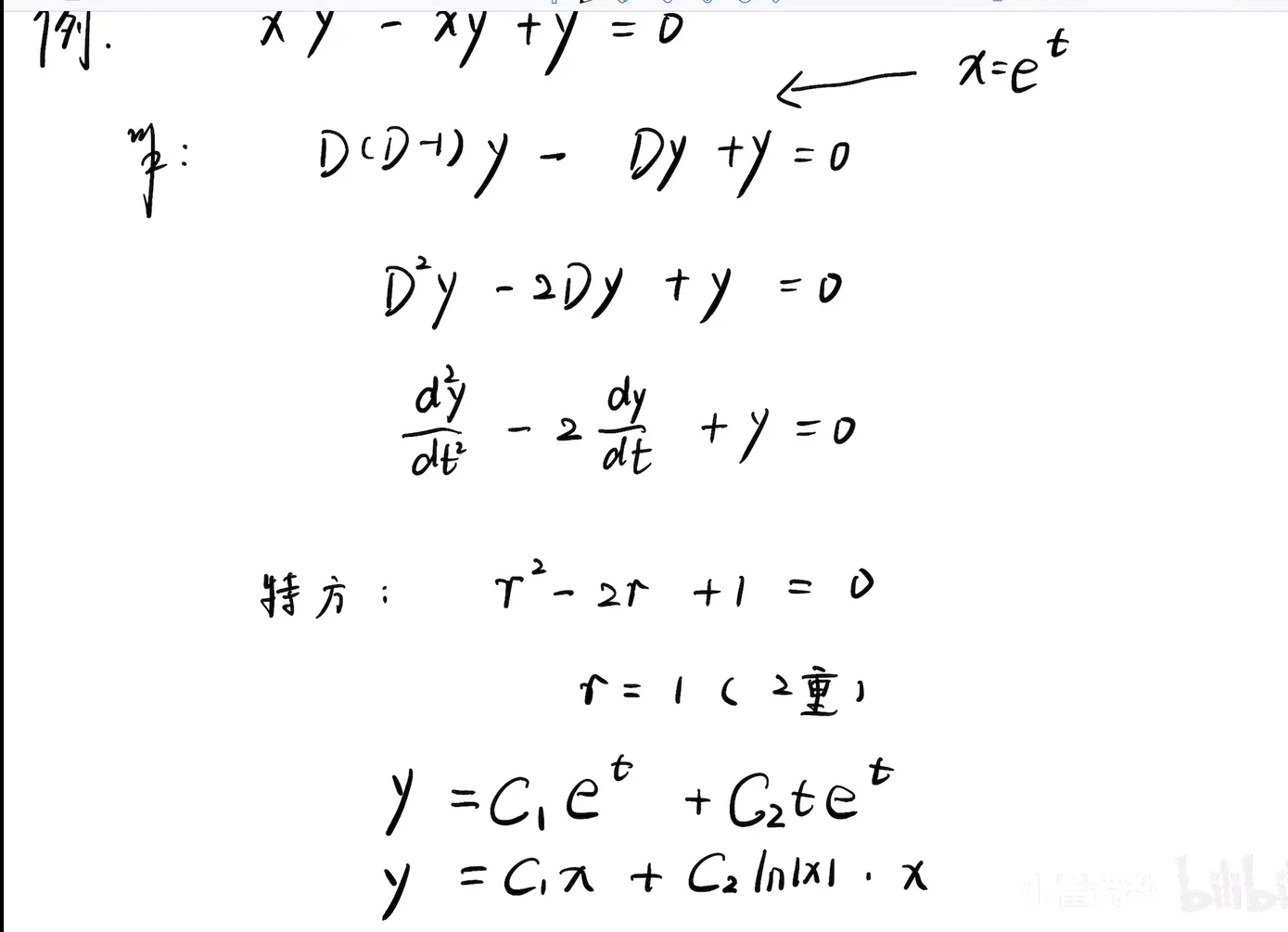
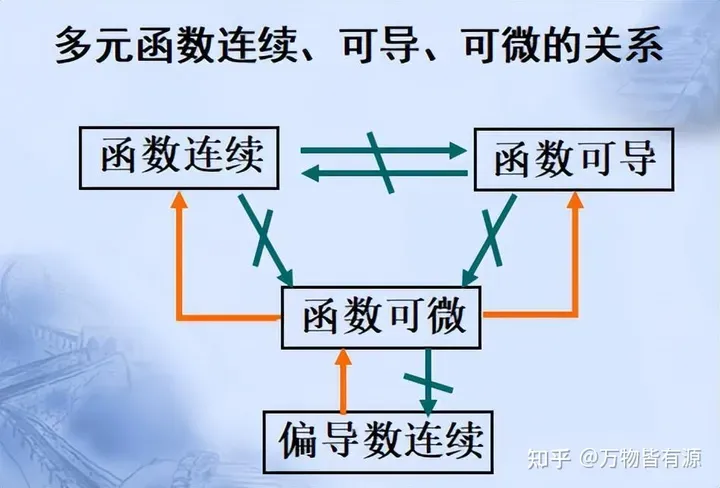
多元函数微分学
全微分p155 用定义判断可微
绝对值不等式:||a|-|b|| ≤ |a±b| ≤ |a|+|b|
无穷级数
如果说明绝对值发散时使用了比值或根值判别,那么可以立即得出原级数发散
绝对收敛±条件收敛=条件收敛
绝对收敛±绝对收敛=绝对收敛
条件收敛±条件收敛=条件收敛或绝对收敛
==求收敛域—>an加绝对值用比值或根值,取倒数==,如果缺项,则用un
级数求导收敛域可能变小,积分可能变大
==幂级数展开P214== p220
==傅里叶级数p224==
向量代数
求a,b为临边的平行四边形面积:S=|a × b|
判定两向量平行:a × b = 0
混合积:(abc)=(a×b)·c 代数表示为行列式
V平行六面体 = |(abc)|
判定三向量共面:(abc)=0
==点到直线距离P233==
==平面束方程== 正常设,然后检验括号里的方程
==两直线距离公式== p236 |s1s2AB|/|s1×s2|
==常见二次曲面== p237 单叶双曲面,双叶双曲面
==建立旋转面方程步骤== p239
==方向导数和梯度== p242 方向导数是一个数(梯度×方向余弦向量) 梯度是一个向量
多元函数积分学
==柱坐标和球坐标== p247
==先一后二 先二后一==
==合一投影法==
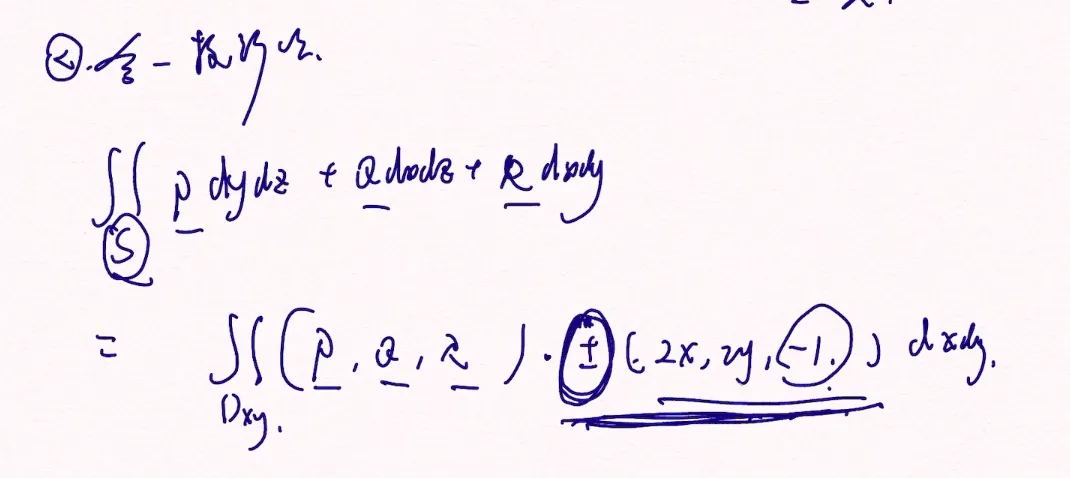
==格林公式 斯托克斯公式 高斯公式== 空间线积分化投影线积分用格林 p262
==梯度散度旋度== p272 梯度是向量 散度是数量PQR偏导之和 旋度是向量(行列式i j k 偏x 偏y 偏z P Q R)
偶零奇倍(二型面积分dxdy)区分 向一个面投影S区域变为D区域
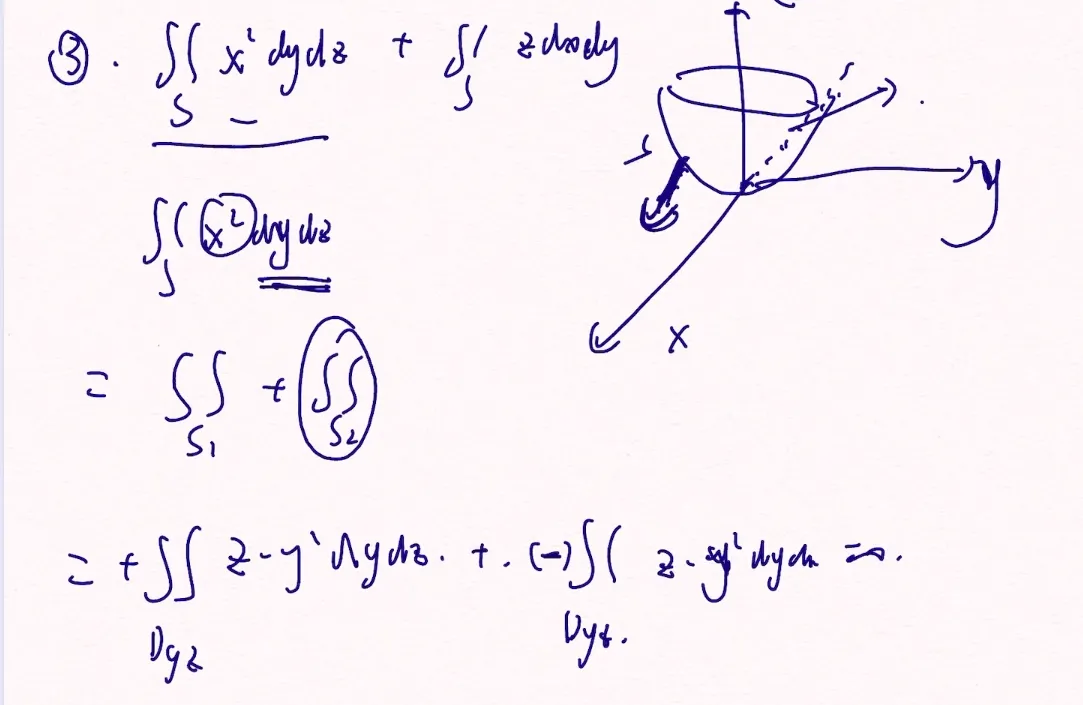
补充:
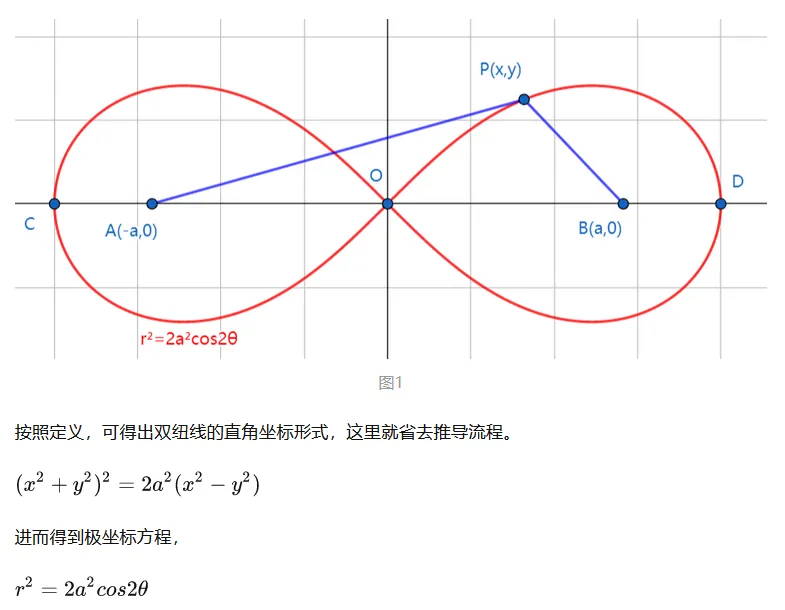
心型线,双扭线 方程
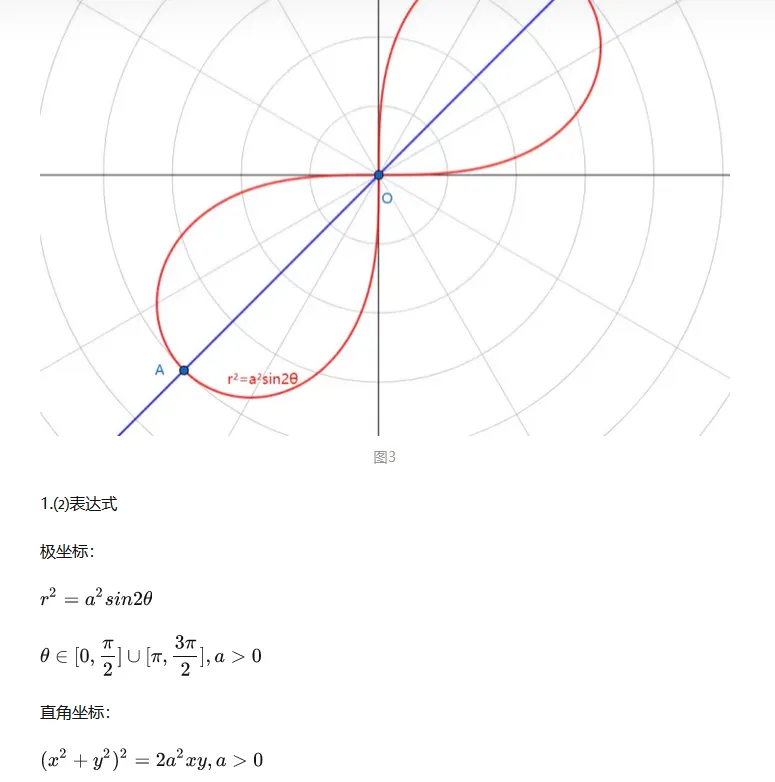
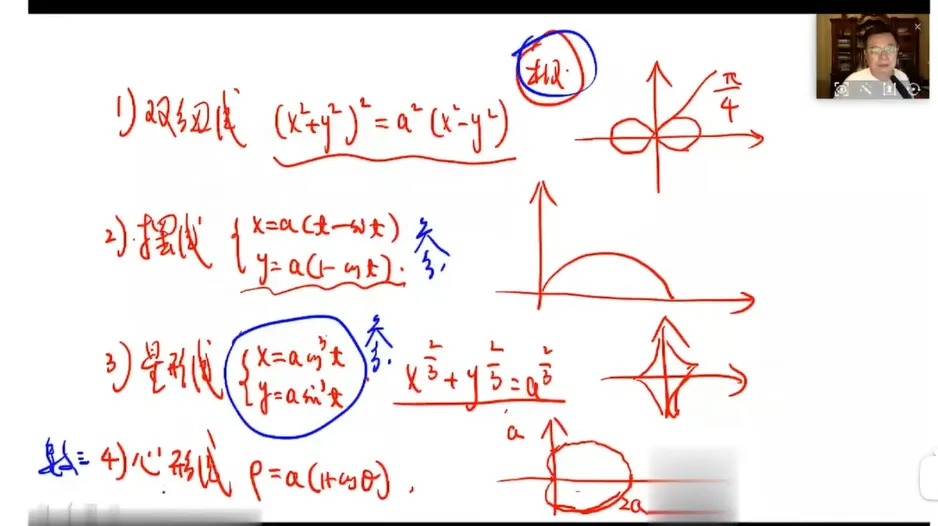
线性代数
行列式
克拉默法则 :
非齐次线性方程组系数行列数不为0,方程组有唯一解
推论:1.齐次方程组系数行列式不为0,方程组只有0解
2.齐次方程组有非零解,则系数行列式为0
数学归纳法
型式1:验证n=1成立,假设n=k成立,证明n=k+1成立;
型式2:验证n=1,n=2成立,假设n<k成立,证明n=k成立
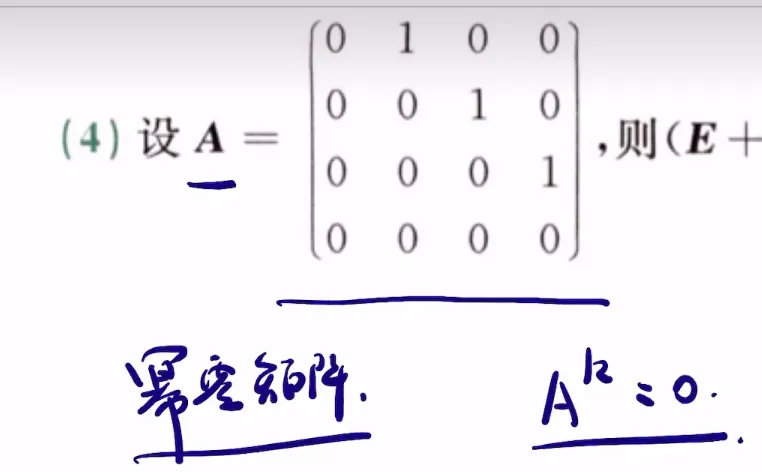
矩阵
重要公式
分块求逆

二阶伴随:主对调负变号
![]()
![]()
A:m×n B
×s ==AB=C专题==
如果A列满秩(r(A)=n),则r(AB)=r(B)
AB的行向量可由B的行向量线性表出 AB的列向量可由A的列向量线性表出
==**AB=0专题 **==
(1)B的每一个列向量都是齐次方程Ax=0的解
(2)r(A) + r(B) ≤ n(A的列数,B的行数)
特殊矩阵
==正交矩阵==
1.A的转置=A的逆矩阵,即ATA=AAT=E
2.==|A|^2 = 1==
3.A,B n阶正交,则AB正交
性质:1.正交矩阵的每个列向量都是单位向量
2.任意两个列向量垂直
3.==正交矩阵一定可逆,|A|不是1就是-1==
==秩1矩阵==
αTβ是矩阵αβT的主对角线元素之和
ααT对称,αTα平方和
总结:A^n = L^(n-1)*A L是矩阵的迹
==秩1矩阵,且迹不为0,则可以相似对角化==
向量
⭐施密特正交化
线性相关线性无关定理 p67 p68
秩的关系
==r(A+B) ≤ r(A,B) ≤ r(A) + r(B)==
r(AB) ≤ min{r(A), r(B)}
同解和公共解
公共解:α既是(I)的解,也是( I)的解,则是公共解
解法:①(I)(II)联立求解 ②求各自基础解系,令相等 ③(I)的通解带入(II)寻找k1,k2关系式
同解:如果α是(I)的解,则必是(II)的解,反过来,如果α是(II)的解,则必是(I)的解
ABx=0与Bx=0同解
同解方程组
==矩阵方程AX=0与BX=0同解的充分必要条是A,B的行向量组等价,即R(A)=R(B)=R(A/B)==
==A,B列向量组等价的充要条件是R(A)=R(B)=R(A,B)==
向量组A=【a1,a2,a3,……】和向量组B=【b1,b2,b3,……】等价的充要条件是rA=rB=r(A,B)。同型矩阵A,B等价的充要条件是rA=rB
特征值与特征向量
对角化
充要条件:①A有n个线性无关特征向量 ②如果λ是k重特征值,那么λ必有k个线性无关特征向量 ③r(λiE - A) = n- ni,λi为ni重特征值
充分条件:A有n个不同的特征值,A是实对称矩阵,则一定可以相似对角化
充分条件:==秩1矩阵,且迹不为0,则可以相似对角化==
实对称矩阵
①必相似对角阵
②可用正交矩阵对角化
③不同特征值的特征向量相互正交
④特征值必是实数
⑤k重特征值必有k个线性无关的特征向量
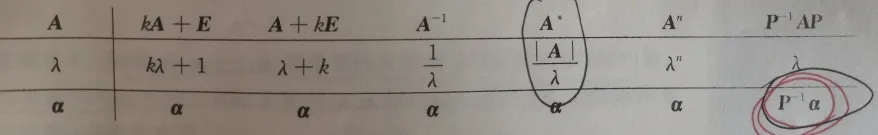
二次型
反对称矩阵对角线元素一定为0
正定
潜台词:一定是对称矩阵
正定一定可逆,因为特征值全>0
充要条件:①特征值全>0 ②正惯性指数p=n ③顺序主子式全>0 ④A=CT E C,c可逆
必要条件:aii>0 |A|>0
矩阵相似等价合同
矩阵等价:Ps…P3P2P1 A Q1Q2…Qt = B => PAQ = B => r(A) = r(B) A经初等变换得到B
同型矩阵等价充要条件:r(A) = r(B)
向量组等价:==A,B列向量组等价的充要条件是R(A)=R(B)=R(A,B)==
向量组A=【a1,a2,a3,……】和向量组B=【b1,b2,b3,……】等价的充要条件是rA=rB=r(A,B)。同型矩阵A,B等价的充要条件是rA=rB
相似
= B 必要条件迹相等,秩相等,行列式相等,|λE-A|=|λE-B|
==判实对称矩阵相似充要条件==:看特征值是否一样
合同:存在可逆矩阵C,使CTAC=B,充要条件是正负惯性指数相同
==相似一定等价,但等价不一定相似==
==实对称矩阵相似一定合同== 实对称矩阵看特征值正负
大数定律与中心极限定理
p110
切比雪夫条件:独立,期望方差存在,方差一致有界
辛钦:独立同分布,期望存在
中心极限定理:列维-林德伯格定理条件:独立同分布,期望方差存在 标准化
数理统计
p118
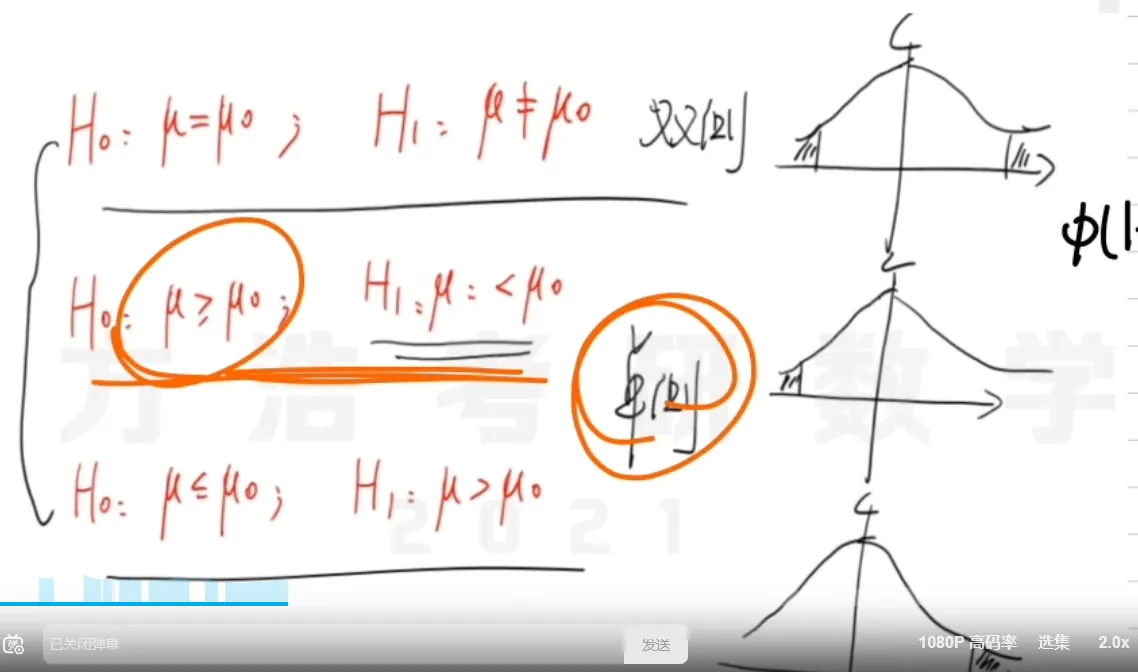
参数估计与假设检验
p134
p140 无偏性 有效性 一致性
p160
李林880题目总结
高等数学
空间几何
两直线之间的距离公式 ——平面束
平面束:
使平面的法向量与L2的方向向量s垂直,求得平面
在L2上找一点,求点到平面的距离,即为两直线距离
正常设,然后检验括号里的方程
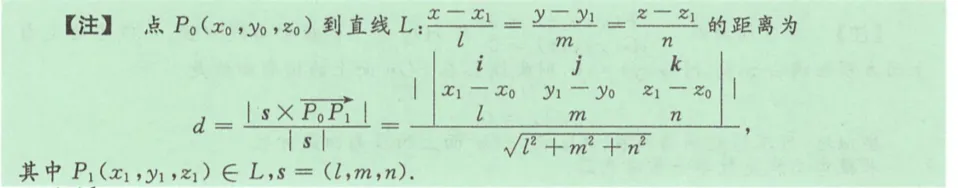
e1×e2 记为n 法向量
==建立旋转面方程==
==无穷级数==

==多元微分p28==
==微分方程伯努利 欧拉 p38==
==中值定理==
线性代数
秩1矩阵
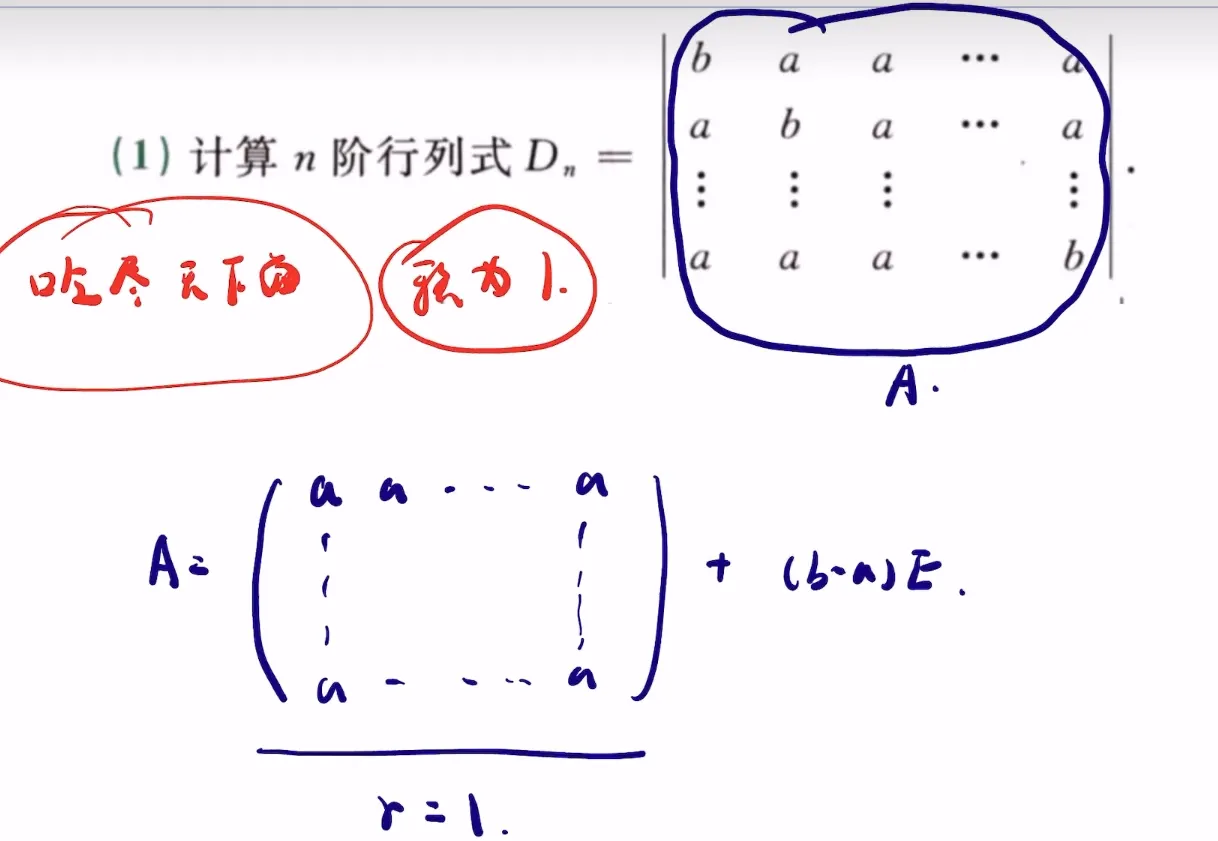 秩1矩阵特征值是主队角元素之和,和n-1个0
秩1矩阵特征值是主队角元素之和,和n-1个0
三对角矩阵
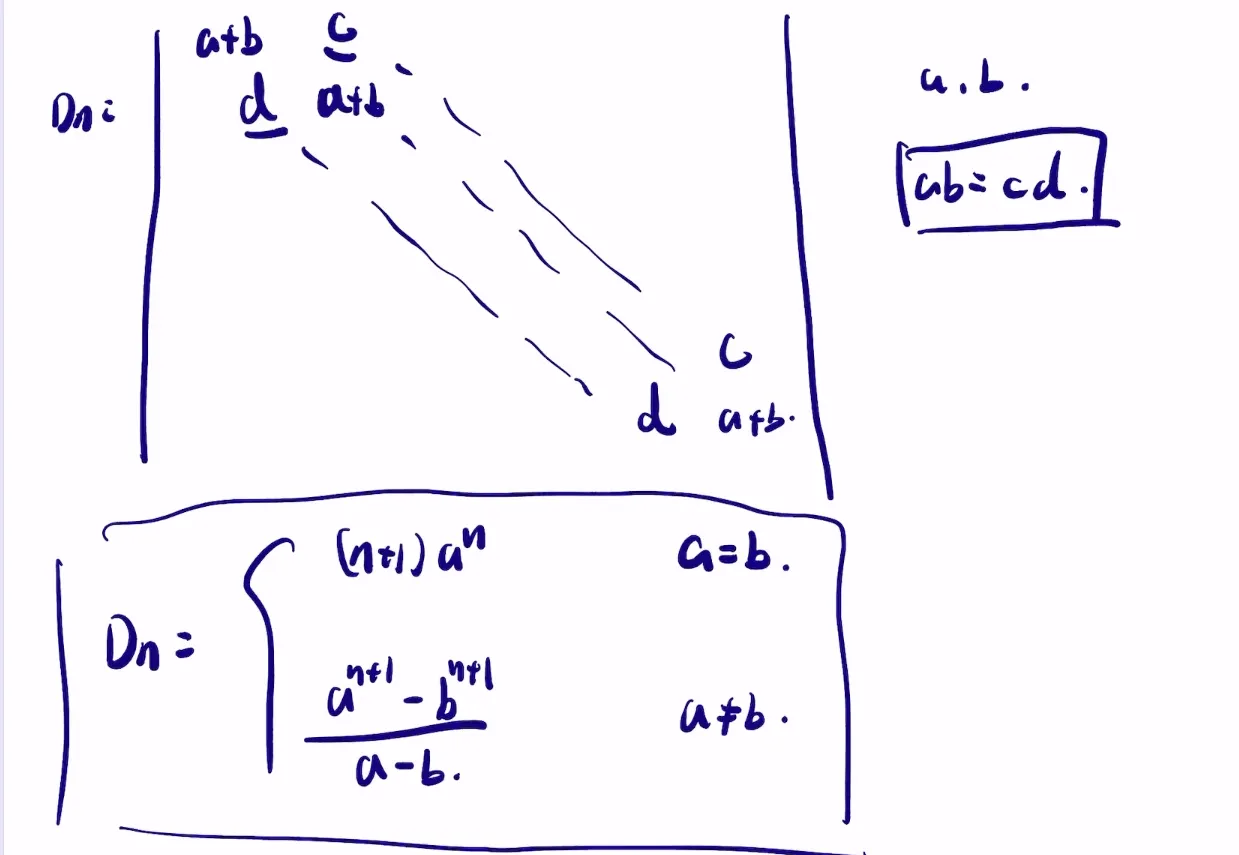
分块矩阵求逆
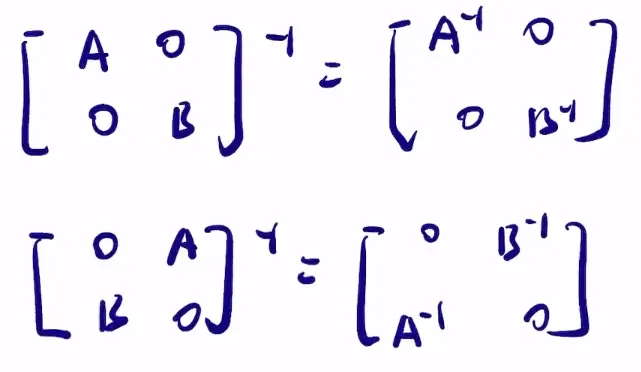
p56 拓展(1)
(AB)T = BT AT
初等矩阵逆矩阵
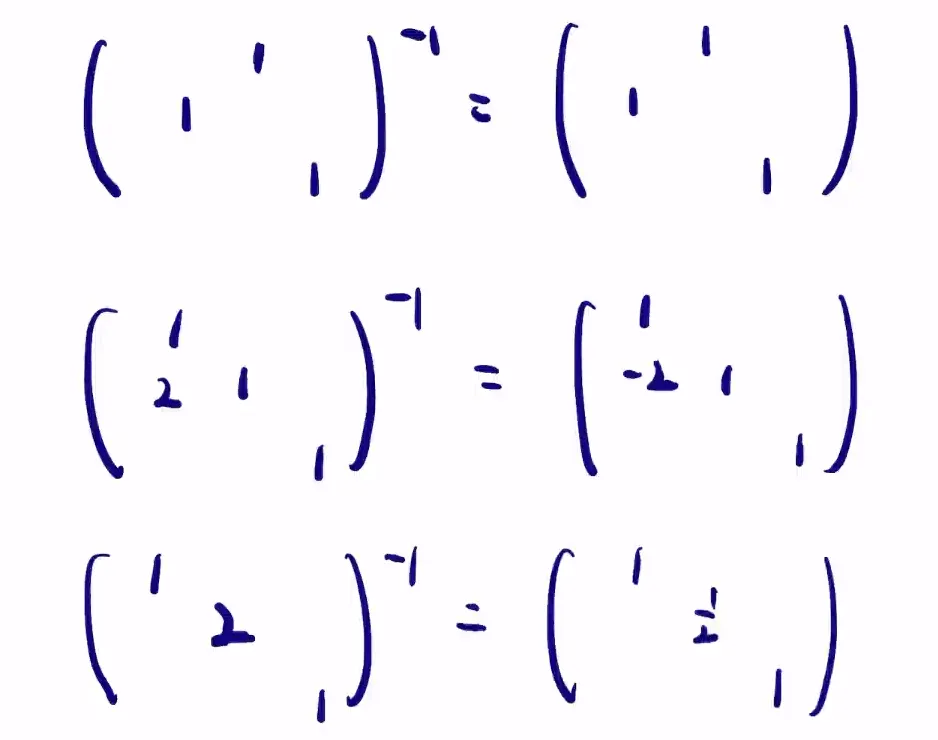
分块矩阵转置

同解方程组

两方程组非零公共解:法1:联立求解 法2:联立基础解系 
两方程组同解:①的通解代入②,解出②的通解,验证①②是否相同
特征向量:重根表示:k1ξ1+k2ξ2 , (k1,k2不同时为0), 单根:k3ξ3 ,(k3不为0) 因为特征向量不为0,而解齐次方程组时,k1k2为任意常数
A^2=A n阶 —> 特征值为0或1 ,r(E-A) + r(A) ≥ r(E) = n, 且A(A-E)= 0 —> r(A)+r(A-E) ≤ n,所以r(A)+r(A-E) = n
写基础解系就写()T,()T 写通解就写k()T+k()T
两正一负是单叶,两负一正是双叶
标准形->规范形
概率论
Y=sinX —–> 2kΠ+(-Π-arcsiny) < x < 2kΠ+arcsiny (关于y=-Π对称) 注意arcsin和arccos的定义域都是[-1,1]
==大数定律中心极限定理==
大数定律:
切比雪夫:独立,期望方差存在,方差一致有界
伯努利
辛钦:独立同分布,期望存在
中心极限定理:
列维林德伯格:独立同分布 期望 方差 ,n很大时,近似服从正态
==数理统计==
t分布的平方服从F(1,n)

 DX的矩估计是二阶中心矩
DX的矩估计是二阶中心矩
==参数估计== 矩估计:X拔等于EX 最大似然估计无极值的情况,L(λ)的导数大于0恒成立,则λ↑,L↑。则λ取max时,最大似然,而λ≤x1,x2…xn,所以λ≤min{x1.x2..xn}, 因此λ取min{x1,x2…xn}
==置信区间:给定一个分布Y,先写出Y拔服从的分布,再标准化==

==假设检验==


==伽马函数==
数学遗忘
方向导数 梯度散度旋度 沿梯度方向的方向导数就是梯度的模 背十遍
等价无穷小1
方向导数:![]()

==常见分布的期望方差== 指数分布期望1/λ 方差1/λ^2 泊松分布期望λ 方差λ
大数定律 中心极限定理 数理统计 参数估计 假设检验
等价相似合同 相似于对角矩阵

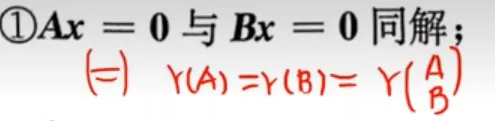

同解方程组 公共解
方向导数

其中cosβ=sinα
方向导数是一个值 若z=f(x,y)可微,则αf/αl=αf/αx·cosα+αf/αy·cosβ
而梯度是一个向量,gradz=(αf/αx,αf/αy)
gradz 点乘 方向余弦 = 方向导数
==傅里叶级数 p224==
==偶零奇倍==
==合一投影法==
先二后一和先一后二
无穷级数背诵 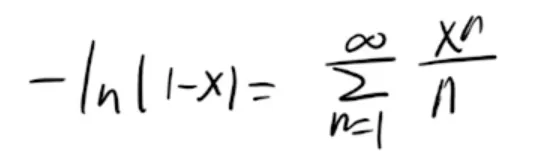 [-1,1)
[-1,1)
二维正态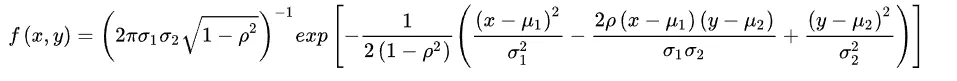
Γ(1) = Γ(2) = 1 Γ(1/2) = 根号Π Γ(n+1) = n!


对应的特征向量:kα1(k≠0)
格林公式用D

球面坐标系